Wenn man unterstellt, dass in Deutschland 2013 das Internet Neuland war und 2001 noch viel unbekannter, welche Wahrscheinlichkeiten können dann den möglichen Ursachen für den Einsturz des World Trade Center zugeordnet werden?
Im Unterschied zum ingenieursmäßigen Szenario wird hier angenommen, dass die TUHH zur Jahrtausendwende kein Ort des Wissenstransfers war, oder dass zumindest im Fall des Kreises um Mohammed Atta der Wissenstransfer und das Erlernen einer für Ingenieure typischen systematischen Arbeitsweise wesentlich gehemmt war.
Dieser Beitrag gehört zu dem Beitrag Zerstörung des WTC im Lichte von Bayes Theorem. Einen populärwissenschaftlichen Text, der Hintergrund und Motivation dieser Berechnungen erläutert, finden Sie hier.
Es geht darum, die Wahrscheinlichkeit der Hypothese VKZAF (= Versuch einer kontrollierten Zerstörung durch Architekten mit Einsatz von Flugzeugen) durch die Anwendung des Bayes Theorem zu bestimmen. Der folgende Text soll also die Begründung liefern für die im folgenden Bild veranschaulichten Verhältnisse:
Das Bild veranschaulicht Eingangsdaten, deren Zahlenwerte im nachfolgenden Text begründet werden. Neben der #Neuland-Prämisse werden hier weitere Hindernisse für eine kontrollierte Zerstörung des WTC postuliert:
- P(VKZA) = 1% (#Neuland-Prämisse)
- P(VKZAF) = 10% * P(VKZA) (Fantastischer Flugzeug-Faktor.) Damit gilt P(VKZAF) = 0,1%, weshalb die linke Urne tausendmal kleiner ist als die rechte. Die Zahlenverhältnisse sind so extrem, dass wir winzige Kugeln von der Größe eines Pixels annehmen müssten. Da kann man auf den Begriff „Kugel“ gleich ganz verzichten und gleich über Pixel sprechen. Die linke Urne soll nur 100.000 Pixel fassen, während rechts ein Ausschnitt einer riesigen Urne gezeigt ist, die 100 Millionen Pixel fasst.
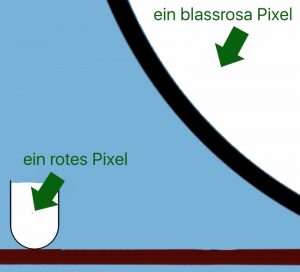
- P(R | VKZAF) = 0,001% (Fort-Knox-Annahme.) Von 100.000 Pixeln ist nur einer rot. Das bringt eine sehr niedrige Erfolgschance für einen Versuch einer kontrollierten Zerstörung zum Ausdruck. Durch Skalierungseffekte ist das rote Pixel nicht unbedingt klar erkennbar.
- P(E | VKZAF) = 10-12. Auf 1000 Milliarden weiße Pixel in der rechten Urne käme nur ein rotes. Das ist angedeutet dardurch, dass ein einzelnes Pixel im Ausschnitt der rechten Urne leicht rosa dargestellt ist. Bei diesen Zahlenverhältnissen müsste man jedes Pixel in 10.000 Teile zerlegen, um rechts ein rotes Teilpixel zu sehen
#Neuland-Prämisse heißt, dass die Attentäter so schlechten Zugang zu Informationen betreffend Zerstörbarkeit des WTC hatten, dass sie nur mit einer Wahrscheinlichkeit von P(VKZA) = 1% eine kontrollierte Zerstörung versuchten.
Fantastischer Flugzeug-Faktor heißt, dass ein nur mit viel Fantasie begründbarer Flugzeugfaktor von 10% angesetzt wird, so dass sich P(VKZA | F) = 10% * P(VKZA) ergibt. Obwohl alle Daten dafür sprechen, dass die Terroristen über einen Überschuß an Attentätern und entführbaren Flugzeugen verfügten, wird hier also ein Mangel daran angenommen um zu schauen was passiert, wenn man alle Annahmen zielgerichtet in eine Richtung verbiegt.
Fort-Knox-Annahme heißt, dass die Büroräume des WTC wie Fort-Knox bewacht waren – auch geschützt vor potentiellen Mietern, die mit Petro-Dollars wedeln konnten. Bei einer intensiven Bewachung wird die Erfolgswahrscheinlichkeit für den Versuch dreier kontrollierter Sprengungen oder Schmelzungen mit P(E | VKSA) = 0,001% abgeschätzt. Dabei bezeichnet das Ereignis E den Erfolg der Gesamtoperation (3 Türme stürzen ein).
Veranschlichung des Volumens der jeweiligen Urnen
Die Eingangsdaten bedeuten, dass die linke Urne sehr viel kleiner ist als die rechte. Denn die Größe der linken Urne entspricht ja der Wahrscheinlichkeit P(VKSA | F) = 10% * P(VKSA) = 10% * 1% = 0,1%
Wenn wir uns vorstellen, dass wir Kugeln mit einem Gesamtvolumen von einem Liter auf beide Urnen verteilen, dann fasst die linke Urne nur einen Milliliter, die rechte Urne die restlichen 0,999 Liter.
Der Anteil der roten Kugeln in der linken Urne beträgt unter der Fort-Knox-Annahme immerhin P(E | VKSA) = 0,001%. Das ist ein kleiner Teil einer winzigen Menge. Das Volumen der in der linken Urne enthaltenen roten Kugeln entspricht also nur dem Hundersten Teil eines Kubikmillimeters. Das entspricht nur 10 Millionen Kubikmikrometern. Und das ist wirklich wenig.
Der Anteil der roten Kugeln in der rechten Urne beträgt, da wir hier keinen Pfusch am Bau annehmen P(E | VKSA) = 10-12. Das Volumen der in der rechten Urne enthaltenen roten Kugeln entspricht also nur dem Volumen eines Würfels mit einer Kantenlänge von 10 Mikrometern.
Wenn wir diese beiden winzigen Mengen vergleichen, dann befinden sich in der linken Urne doch Zehntausend mal so viele rote Kugeln wie in der rechten Urne.
Wenn wir also wissen, dass wir eine rote Kugel gezogen haben, dann wird diese mit Sicherheit (genauer: Zehntausend zu Eins) aus der linken Urne entstammen.